手动开根的应用

以前没想过写这篇文章，但是自打上次考试在一元二次方程用公式法里用这个开出 $\sqrt{129600}$ 以后……

#方法一：短除法

（本方法由同学总结）

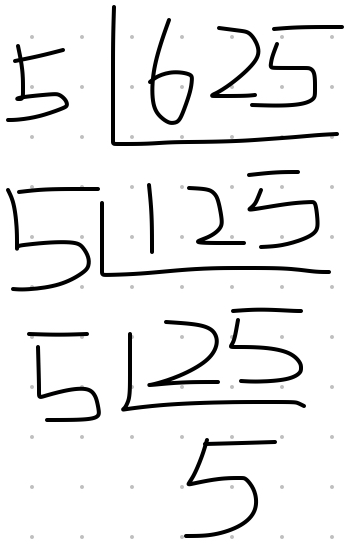
（手写，字丑勿喷（））
可得， $625=5\times 5\times 5\times 5$

将这4个5分成2部分，即得到 $625=(5\times 5)\times (5\times 5)=25\times 25$ 。

故$\sqrt{625}=25$

这种方法适用于被开方数正好是一个整数的平方。

#方法二：公式法

（笔算不推荐）
$ \Large{x_{n+1}=\frac{x_n+\frac{a}{x_n}}{2}} $

具体见此（人话：这个方法我也不会）：https://zhuanlan.zhihu.com/p/378906296

#方法三：竖式开根

我们令被开方数为$1342$

#1. 列出竖式

$\sqrt{1342}$

#2.从小数点开始，每两个数分为一组

$\sqrt{13\ 42}$
如果遇到单数位怎么办：
$\sqrt{3\ 42}$
小数部分也一样，只不过是从小数点往右推
$\sqrt{3\ 42.55\ 4}$

#3. 求解开方第一组数的近似值

$$ \quad\ 3\newline 3\sqrt{13}\newline \quad\frac{\quad 9}{\quad 4} $$

根号顶上的3和根号左边的3代表 $3\times 3$ ，其结果9写在13的下面，将$13-9$的结果4带下来。
注意，根号顶上的3一定要写在两位数（本例中的13）中间！

#4.后面该怎么计算？

$$ \quad 3\ \textcolor{red}{\Box}\newline 3\sqrt{13\ 42}\newline \quad 9\newline \textcolor{red}{6\Box}\sqrt{4\ 42} $$

红色区域的两数相乘的积，得小于442，同时取最大值。

而为什么是$6\Box\times \Box$？为何取6？请观察根号顶端方框前面的数：是数字3¹。
我们用$3\times 2$，得到6。

多次计算可得，$66\times 6$小于442，是表达式最大值。

得：

$$ \quad\ 3\quad 6\\ 3\sqrt{13\ 42}\\ \quad 9\\ \ 66\sqrt{4\ 42}\\ \quad\quad\frac{\ 3\ 96}{\quad 46} $$

继续向下计算，得 $\sqrt{1342}\approx 36.633$